6-3 円錐図法
地球に円錐をかぶせて投影する図法で、地球にぴったりかぶせた接円錐と地球に円錐を
挿入した割(二基本緯線)円錐がある。
<接円錐図法> <割円錐図法>

6-3-1 Equidistant Conic (正距円錐図法)
【 投影式 】 φ0 = ( φ1 + φ2 ) / 2
n = (cosφ1 - cosφ2) / (φ2 - φ1)
ρ = R [ (φ2 cosφ1 - φ1 cosφ2) / ( cosφ1 - cosφ2) - φ]
ρ0 = R [ (φ2 cosφ1 - φ1 cosφ2) / ( cosφ1 - cosφ2) - φ0]
θ = n ( λ - λ0 )
x = ρ sin θ
y = ρ0 - ρ cos θ
【経線・緯線】 経線:直線 、緯線:曲線
【 ポイント 】・経線は、左右端の経度が同じなので片方の経線の
「補正λ-λ0」の不等号に「=」を付けて対応する。
(参照 別項 1-3 )
| <基準経度・標準緯度・予備計算・共通数値 など> | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| λ0 | C2 | ??? ← 中心経度(希望経度を入力) | ||||||||||||||||||||||||||||||||||
| φ1 | C3 | ?? ← 標準緯度1(希望緯度を入力) | ||||||||||||||||||||||||||||||||||
| φ2 | C4 | ?? ← 標準緯度2(希望緯度を入力) | ||||||||||||||||||||||||||||||||||
| R | C5 | 1 ← 描画係数 | ||||||||||||||||||||||||||||||||||
| φ0 | G2 | =(C3+C4)/2 ← 中央緯度 | ||||||||||||||||||||||||||||||||||
| ρ0 | G3 |
=(RADIANS($C$4)*COS(RADIANS($C$3))-RADIANS($C$3)* COS(RADIANS($C$4)))/(COS(RADIANS($C$3))- COS(RADIANS($C$4)))-RADIANS($G$2) |
||||||||||||||||||||||||||||||||||
| n | G4 | =(COS(RADIANS($C$3))-COS(RADIANS($C$4)))/(RADIANS($C$4-$C$3)) | ||||||||||||||||||||||||||||||||||
| <データ計算 など> 経度緯度のデータ毎に記述式を複写(行コピー)する。 | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| No. | B9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | C9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | D9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
|
補正 λ-λ0 |
E9 |
=IF($C$2<0,IF(C9-$C$2>180,C9-$C$2-360,C9-$C$2), IF(C9-$C$2<-180,C9+360-$C$2,C9-$C$2)) |
||||||||||||||||||||||||||||||||||
| ρ | F9 |
=(RADIANS($C$4)*COS(RADIANS($C$3))-RADIANS($C$3)* COS(RADIANS($C$4)))/(COS(RADIANS($C$3))- COS(RADIANS($C$4)))-RADIANS(D9) |
||||||||||||||||||||||||||||||||||
| x | G9 | =F9*SIN($G$4*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| y | H9 | =$G$3-F9*COS($G$4*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| 端CH | I10 |
=IF(G10="",0,IF(AND(ABS(G10)>0.2,G9*G10<0),"●", IF(AND(G9<>"",G10>PI()/2,ABS(G9-G10)>0.2),"●",0))) |
||||||||||||||||||||||||||||||||||
| ↑ 左右の端をチェックしている。"●"の付いた行の前に一行挿入すると、勝手に左端と右端が線で結ばれない。 | ||||||||||||||||||||||||||||||||||||
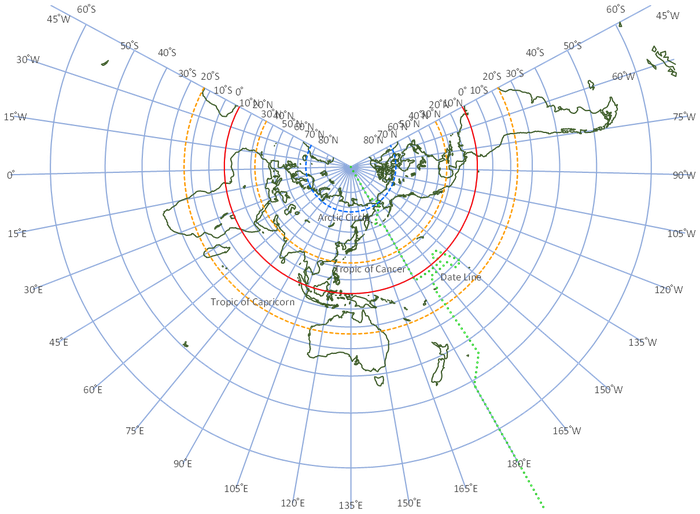
[図 6-3-1] 正距円錐図法 ( Equidistant Conic Projection )
【地図主点(中心)】東経 135゚ 【標準緯度1】北緯20゚【標準緯度2】北緯40゚
【経度間隔】15゚【緯度間隔】10゚
6-3-2 Albers Equal-Area Conic (アルベルス正積円錐図法)
【 投影式 】 k = ( sinφ1 + sinφ2) / 2
r = R ( 1 + sinφ1 sinφ2 - 2 k sinφ)1/2 / k
x = r sin( k ( λ - λ0 ))
y = - r cos( k ( λ - λ0 ))
【経線・緯線】 経線:直線 、緯線:曲線
【 ポイント 】・経線は、左右端の経度が同じなので片方の経線の
「補正λ-λ0」の不等号に「=」を付けて対応する。
(参照 別項 1-3 )
| <基準経度・標準緯度・予備計算・共通数値 など> | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| λ0 | C2 | ??? ← 中心経度(希望経度を入力) | ||||||||||||||||||||||||||||||||||
| φ1 | C3 | ?? ← 標準緯度1(希望緯度を入力) | ||||||||||||||||||||||||||||||||||
| φ2 | C4 | ?? ← 標準緯度2(希望緯度を入力) | ||||||||||||||||||||||||||||||||||
| R | C5 | 1 ← 描画係数 | ||||||||||||||||||||||||||||||||||
| <データ計算 など> 経度緯度のデータ毎に記述式を複写(行コピー)する。 | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| No. | B9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | C9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | D9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
|
補正 λ-λ0 |
E9 |
=IF($C$2<0,IF(C9-$C$2>180,C9-$C$2-360,C9-$C$2), IF(C9-$C$2<-180,C9+360-$C$2,C9-$C$2)) |
||||||||||||||||||||||||||||||||||
| k | F9 | =(SIN(RADIANS($C$3))+SIN(RADIANS($C$4)))/2 | ||||||||||||||||||||||||||||||||||
| r | G9 |
=SQRT(1+SIN(RADIANS($C$3))* SIN(RADIANS($C$4))-2*F9*SIN(RADIANS(D9)))/F9 |
||||||||||||||||||||||||||||||||||
| x | H9 | =G9*SIN(F9*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| y | I9 | =-G9*COS(F9*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| 端CH | J10 |
=IF(H10="",0,IF(AND(ABS(H10)>0.2,H9*H10<0),"●", IF(AND(H9<>"",H10>PI()/2,ABS(H9-H10)>0.2),"●",0))) |
||||||||||||||||||||||||||||||||||
| ↑ 左右の端をチェックしている。"●"の付いた行の前に一行挿入すると、勝手に左端と右端が線で結ばれない。 | ||||||||||||||||||||||||||||||||||||
[図 6-3-2] アルベルス正積円錐図法 ( Albers Equal-area Conic Projection )
【地図主点(中心)】東経 135゚ 【標準緯度1】北緯20゚【標準緯度2】北緯40゚ 【経度間隔】15゚【緯度間隔】10゚
6-3-3 Lambert Equal-Area Conic (ランベルト正積円錐図法)
【 投影式 】 k = ( 1 + sinφ0) / 2
r = R [ ( 2 ( 1 - sinφ) / k ] 1/2
x = r sin( k ( λ - λ0 ))
y = - r cos( k ( λ - λ0 ))
【経線・緯線】 経線:直線 、緯線:曲線
【 ポイント 】・経線は、左右端の経度が同じなので片方の経線の
「補正λ-λ0」の不等号に「=」を付けて対応する。
(参照 別項 1-3 )。
| <基準経度・標準緯度・予備計算・共通数値 など> | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| λ0 | C2 | ??? ← 中心経度(希望経度を入力) | ||||||||||||||||||||||||||||||||||
| φ0 | C3 | ?? ← 標準緯度0 (希望緯度0 を入力) | ||||||||||||||||||||||||||||||||||
| R | C4 | 1 ← 描画係数 | ||||||||||||||||||||||||||||||||||
| <データ計算 など> 経度緯度のデータ毎に記述式を複写(行コピー)する。 | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| No. | B9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | C9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | D9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
|
補正 λ-λ0 |
E9 |
=IF($C$2<0,IF(C9-$C$2>180,C9-$C$2-360,C9-$C$2), IF(C9-$C$2<-180,C9+360-$C$2,C9-$C$2)) |
||||||||||||||||||||||||||||||||||
| k | F9 | =(1+SIN(RADIANS($C$3)))/2 | ||||||||||||||||||||||||||||||||||
| r | G9 | =SQRT((2*(1-SIN(RADIANS(D9)))/F9)) | ||||||||||||||||||||||||||||||||||
| x | H9 | =G9*SIN(F9*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| y | I9 | =-G9*COS(F9*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| 端CH | J10 |
=IF(H10="",0,IF(AND(ABS(H10)>0.2,H9*H10<0),"●", IF(AND(H9<>"",H10>PI()/2,ABS(H9-H10)>0.2),"●",0))) |
||||||||||||||||||||||||||||||||||
| ↑ 左右の端をチェックしている。"●"の付いた行の前に一行挿入すると、勝手に左端と右端が線で結ばれない。 | ||||||||||||||||||||||||||||||||||||
[図 6-3-3] ランベルト正積円錐図法 ( Lambert equal-area conic projection )
【地図主点(中心)】東経 135゚ 【標準緯度】北緯30゚ 【経度間隔】15゚【緯度間隔】10゚
6-3-4 Lambert Conformal Conic (ランベルト正角円錐図法)
【 投影式 】 n = In (cosφ1 secφ2) / ln [ tan(π/4 +φ2 /2 ) cot(π/4 +φ1/2 )]
F = [cosφ1 tann (π/4+φ1/2)] / n
ρ = F cotn (π/4 +φ/2)
ρ0= F cotn (π/4 +φ0/2)
x = ρ sin [ n (λ - λ0) ]
y = ρ0 - ρ cos [ n (λ - λ0) ]
【経線・緯線】 経線:直線 、緯線:曲線
【 ポイント 】・φ0 は、参照緯度であるが、この数値は y軸 方向へのシフトを
コントロールしている。投影形状自体には影響しないので、
私は 90°として描画した。
・中心となる極から離れるにつれ、緯度間隔が増加して歪むので
適当な緯度までの描画とする。
・経線は、左右端の経度が同じなので片方の経線の「補正λ-λ0」
の不等号に「=」を付けて対応する。
(参照 別項 1-3 )
| <基準経度・標準緯度・予備計算・共通数値 など> | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| λ0 | C2 | ??? ← 中心経度(希望経度を入力) | ||||||||||||||||||||||||||||||||||
| φ0 | C3 | 90 ← 上記「ポイント」参照 | ||||||||||||||||||||||||||||||||||
| φ1 | C4 | ?? ← 標準緯度1(希望緯度1 を入力) | ||||||||||||||||||||||||||||||||||
| φ2 | C5 | ?? ← 標準緯度2(希望緯度2 を入力) | ||||||||||||||||||||||||||||||||||
| n | G2 |
=LN(COS(RADIANS($C$4))*SEC(RADIANS($C$5)))/LN(TAN(PI()/4+ RADIANS($C$5)/2)*COT(PI()/4+RADIANS($C$4)/2)) |
||||||||||||||||||||||||||||||||||
| F | G3 | =(COS(RADIANS($C$4))*(TAN(PI()/4+RADIANS($C$4)/2)^$G$2))/$G$2 | ||||||||||||||||||||||||||||||||||
| ρ0 | G4 | =$G$3*COT(PI()/4+RADIANS($C$3)/2)^$G$2 | ||||||||||||||||||||||||||||||||||
| <データ計算 など> 経度緯度のデータ毎に記述式を複写(行コピー)する。 | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| No. | B9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | C9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | D9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
|
補正 λ-λ0 |
E9 |
=IF($C$2<0,IF(C9-$C$2>180,C9-$C$2-360,C9-$C$2), IF(C9-$C$2<-180,C9+360-$C$2,C9-$C$2)) |
||||||||||||||||||||||||||||||||||
| ρ | F9 | =$G$3*COT(PI()/4+RADIANS(D9)/2)^$G$2 | ||||||||||||||||||||||||||||||||||
| x | G9 | =F9*SIN($G$2*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| y | H9 | =$G$4-F9*COS($G$2*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| 端CH | I10 |
=IF(G10="",0,IF(AND(ABS(G10)>0.2,G9*G10<0),"●", IF(AND(G9<>"",G10>PI()/2,ABS(G9-G10)>0.2),"●",0))) |
||||||||||||||||||||||||||||||||||
| ↑ 左右の端をチェックしている。"●"の付いた行の前に一行挿入すると、勝手に左端と右端が線で結ばれない。 | ||||||||||||||||||||||||||||||||||||
[図 6-3-4] ランベルト正角円錐図法 ( Lambert Conformal Conic Projection )
【地図主点(中心)】東経 135゚ 【標準緯度1】北緯20゚【標準緯度2】北緯40゚
【経度間隔】15゚【緯度間隔】10゚
【地図主点(中心)】東経 135゚ 【標準緯度1】北緯20゚【標準緯度2】北緯60゚
【経度間隔】15゚【緯度間隔】10゚
6-3-5 Perspective Conic (心射円錐図法)
【 投影式 】φ0 = ( φ1 + φ2 ) / 2
もし φ<= φ0 - 90° and φ0 > 0
あるいは φ>= φ0 + 90° and φ0 < 0 なら
その point は描画しない。
それ以外の場合は
n = sin φ0
ρ = R cos [(φ2 - φ1)/2 )] [cot φ0 - tan (φ- φ0 )]
ρ0 = R [(φ2 cosφ1 - φ1 cos φ2 ) / (cosφ1 - cosφ2)- φ0]
θ = n ( λ- λ0 )
x = ρ sin θ
y = ρ0 - ρ cos θ
【経線・緯線】 経線:直線 、緯線:曲線
【 ポイント 】・経線は、左右端の経度が同じなので片方の経線の
「補正λ-λ0」の不等号に「=」を付けて対応する。
(参照 別項 1-3 )
| <基準経度・標準緯度・予備計算・共通数値 など> | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| λ0 | C2 | ??? ← 中心経度(希望経度を入力) | ||||||||||||||||||||||||||||||||||
| φ1 | C3 | ?? ← 標準緯度1(希望緯度1 を入力) | ||||||||||||||||||||||||||||||||||
| φ2 | C4 | ?? ← 標準緯度2(希望緯度2 を入力) | ||||||||||||||||||||||||||||||||||
| φ0 | C5 | =(C3+C4)/2 | ||||||||||||||||||||||||||||||||||
| R | C6 | 1 | ||||||||||||||||||||||||||||||||||
| ρ0 | G2 |
=(RADIANS($C$4)*COS(RADIANS($C$3))-RADIANS($C$3)* COS(RADIANS($C$4)))/(COS(RADIANS($C$3))- COS(RADIANS($C$4)))-RADIANS($C$5) |
||||||||||||||||||||||||||||||||||
| n | G3 | =SIN(RADIANS($C$5)) | ||||||||||||||||||||||||||||||||||
| <データ計算 など> 経度緯度のデータ毎に記述式を複写(行コピー)する。 | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| No. | B9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | C9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | D9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
|
補正 λ-λ0 |
E9 |
=IF($C$2<0,IF(C9-$C$2>180,C9-$C$2-360,C9-$C$2), IF(C9-$C$2<-180,C9+360-$C$2,C9-$C$2)) |
||||||||||||||||||||||||||||||||||
| ρ | F9 | =COS(RADIANS(($C$4-$C$3)/2))*(COT(RADIANS($C$5))-TAN(RADIANS(D9-$C$5))) | ||||||||||||||||||||||||||||||||||
| x | G9 | =F9*SIN($G$3*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| y | H9 | =$G$4-F9*COS($G$2*RADIANS(E9)) | ||||||||||||||||||||||||||||||||||
| 描画CH | I9 | =IF(OR(AND(D9<$C$5-90,$C$5>0),AND(D9>$C$5+90,$C$5<0)),"●",0) | ||||||||||||||||||||||||||||||||||
| 端CH | J10 |
=IF(G10="",0,IF(AND(ABS(G10)>0.2,G9*G10<0),"●", IF(AND(G9<>"",G10>PI()/2,ABS(G9-G10)>0.2),"●",0))) |
||||||||||||||||||||||||||||||||||
|
↑ └← 端CH:左右の端をチェックしている。"●"の付いた行の前に一行挿入すると、勝手に ↑ 左端と右端が線で結ばれない。
↑ 消去する。 |
||||||||||||||||||||||||||||||||||||
[図 6-3-5] Perspective Conic 図法 ( Perspective Conic Projection )
【地図主点(中心)】東経 135゚【標準緯度1】北緯20゚【標準緯度2】北緯40゚
【経度間隔】15゚【緯度間隔】10゚
【地図主点(中心)】東経 135゚【標準緯度1】北緯20゚【標準緯度2】北緯60゚
【経度間隔】15゚【緯度間隔】10゚
6-3-6 Normal Polyconic (正規多円錐図法)
【 投影式 】x = R cotφsin [ (λ - λ0) sinφ]
y = R <φ+ cotφ{1 – cos [ (λ - λ0) sinφ] } >
但し φ = 0 ⇒ x = λ - λ0 , y = 0
【経線・緯線】 経線:曲線 、緯線:曲線
【 ポイント 】・経線は、左右端の経度が同じなので片方の経線の
「補正λ-λ0」の不等号に「=」を付けて対応する。
(参照 別項 1-3 )。
| <基準経度・標準緯度・予備計算・共通数値 など> | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| λ0 | C2 | ??? ← 中心経度(希望経度を入力) | ||||||||||||||||||||||||||||||||||
| R | C3 | 1 ← 描画係数 | ||||||||||||||||||||||||||||||||||
| <データ計算 など> 経度緯度のデータ毎に記述式を複写(行コピー)する。 | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| No. | B9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | C9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | D9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
|
補正 λ-λ0 |
E9 |
=IF($C$2<0,IF(C9-$C$2>180,C9-$C$2-360,C9-$C$2), IF(C9-$C$2<-180,C9+360-$C$2,C9-$C$2)) |
||||||||||||||||||||||||||||||||||
| x | F9 | =COT(RADIANS(D9))*SIN((RADIANS(E9)*SIN(RADIANS(D9)))) | ||||||||||||||||||||||||||||||||||
| y | G9 | =RADIANS(D9)+COT(RADIANS(D9))*(1-COS(RADIANS(E9)*SIN(RADIANS(D9)))) | ||||||||||||||||||||||||||||||||||
| 端CH | H10 |
=IF(F10="",0,IF(AND(ABS(F10)>0.2,F9*F10<0),"●", IF(AND(F9<>"",F10>PI()/2,ABS(F9-F10)>0.2),"●",0))) |
||||||||||||||||||||||||||||||||||
| ↑ 左右の端をチェックしている。"●"の付いた行の前に一行挿入すると、勝手に左端と右端が線で結ばれない。 | ||||||||||||||||||||||||||||||||||||
[図 6-3-6] 正規多円錐図法 ( Normal Polyconic Projection )
【地図主点(中心)】東経 135゚、緯度 0゚ 【経度間隔】15゚【緯度間隔】10゚
6-3-7 Rectangular Polyconic Projection (直交多円錐図法)
【 投影式 】正距とする緯線をφ1とすると
φ1 = 0 なら A = ( λ - λ0) / 2
φ1 ≠ 0 なら A = tan{ [ ( λ - λ0 ) sinφ1 ] / 2 } / sinφ1
x = R cotφsin [ 2 arctan ( A sinφ)]
y = R《φ+ cotφ{1 - cos [ 2 arctan ( A sinφ) ] } 》
但し φ = 0 ⇒ x = 2 R A , y = 0
【経線・緯線】 経線:曲線 、緯線:曲線
【 ポイント 】・経線と緯線は、直交する。
・経線は、左右端の経度が同じなので片方の経線の
「補正λ-λ0」の不等号に「=」を付けて対応する。
(参照 別項 1-3 )。
| <基準経度・標準緯度・予備計算・共通数値 など> | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| λ0 | C2 | ??? ← 中心経度(希望経度を入力) | ||||||||||||||||||||||||||||||||||
| φ1 | C3 | ?? ← 正距とする緯度(希望緯度 を入力) | ||||||||||||||||||||||||||||||||||
| R | C4 | 1 ← 描画係数 | ||||||||||||||||||||||||||||||||||
| <データ計算 など> 経度緯度のデータ毎に記述式を複写(行コピー)する。 | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| No. | B9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | C9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | D9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
|
補正 λ-λ0 |
E9 |
=IF($C$2<0,IF(C9-$C$2>180,C9-$C$2-360,C9-$C$2), IF(C9-$C$2<-180,C9+360-$C$2,C9-$C$2)) |
||||||||||||||||||||||||||||||||||
| A | F9 |
=IF($C$3=0,RADIANS(E9)/2,TAN((RADIANS(E9)* SIN(RADIANS($C$3)))/2)/SIN(RADIANS($C$3))) |
||||||||||||||||||||||||||||||||||
| x | G9 | =IF(D9=0,2*F9,COT(RADIANS(D9))*SIN(2*ATAN((F9*SIN(RADIANS(D9)))))) | ||||||||||||||||||||||||||||||||||
| y | H9 |
=IF(D9=0,0,RADIANS(D9)+COT(RADIANS(D9))* (1-COS(2*ATAN(F9*SIN(RADIANS(D9)))))) |
||||||||||||||||||||||||||||||||||
| 端CH | I10 |
=IF(G10="",0,IF(AND(ABS(G10)>0.2,G9*G10<0),"●", IF(AND(G9<>"",G10>PI()/2,ABS(G9-G10)>0.2),"●",0))) |
||||||||||||||||||||||||||||||||||
| ↑ 左右の端をチェックしている。"●"の付いた行の前に一行挿入すると、勝手に左端と右端が線で結ばれない。 | ||||||||||||||||||||||||||||||||||||
[図 6-3-7] 直交多円錐図法 ( Rectangular Polyconic Projection )
【地図主点(中心)】東経 135゚、緯度 0゚ 【正距緯度】 0゚【経度間隔】15゚【緯度間隔】10゚
【地図主点(中心)】東経 135゚、緯度 0゚ 【正距緯度】 30゚【経度間隔】15゚【緯度間隔】10゚
6-3-8 Interrupted Normal Polyconic (断裂多円錐図法・舟底型多円錐図法)
【 投影式 】 λcは舟形範囲中央経度とすると
x = R cotφsin( (λ - λc) sinφ)
y = R {φ+ cotφ[1 - cos ( (λ - λc) sinφ) ] }
但し φ = 0 ⇒ x = λ -λc , y = 0
【経線・緯線】 経線:曲線 、緯線:曲線
【 ポイント 】・正規多円錐図法を断裂させて描画したもので断裂させた
ブロックの中央経度を λC として算出し、各々をシフト
結合させる。
・断裂ブロックの経度幅は、描画経度単位の10°、15°の
倍数とすると船形の端に経線が来る。
・ブロックの左右端経度、中央経度を整理して算出する
(下図に例を示す)。
・極に近い部分の補正はしていません。

記述式はブロック単位で複雑となるためエクセル画面の例をイメージとしてみました。

| <基準経度・標準緯度・予備計算・共通数値 など> | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| 分断数 | C2 | ?? ← 前述【ポイント】参照 | ||||||||||||||||||||||||||||||||||
| R | C3 | 1 ← 描画係数 | ||||||||||||||||||||||||||||||||||
| ブロック幅 | G2 | =360/C2 ← ←←← 単位は「°」 | ||||||||||||||||||||||||||||||||||
| ブロック幅変換 | G3 | =RADIANS(G2) ←ラジアン変換 ( ブロックのシフト幅 ) | ||||||||||||||||||||||||||||||||||
| <データ計算 など> 経度緯度のデータ毎に記述式を複写(行コピー)する。 | ||||||||||||||||||||||||||||||||||||
| 記号 | セルNo. | 記述式 | ||||||||||||||||||||||||||||||||||
| ブロック | C6 | 1 ← ブロック番号を入力する | ||||||||||||||||||||||||||||||||||
| λC | C7 | -15 ← ブロックの中央経度を入力する | ||||||||||||||||||||||||||||||||||
| No. | B9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | C9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | D9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
| x | E9 |
=IF(D9=0,RADIANS(C9-C$7),COT(RADIANS(D9))* SIN((RADIANS(C9-C$7)*SIN(RADIANS(D9))))) |
||||||||||||||||||||||||||||||||||
| y | F9 |
=IF(D9=0,0,RADIANS(D9)+COT(RADIANS(D9))* (1-COS(RADIANS(C9-C$7)*SIN(RADIANS(D9))))) |
||||||||||||||||||||||||||||||||||
| ブロック | H6 | 2 ← 次のブロック番号を入力する | ||||||||||||||||||||||||||||||||||
| λC | H7 | 15 ← 次のブロックの中央経度を入力する | ||||||||||||||||||||||||||||||||||
| No. | G9 | ??? ← 式を複写する時に、一旦ソートしたり、解析時に役立つので連番号を付与 | ||||||||||||||||||||||||||||||||||
| 経度 | H9 | ??? ← 実際の経度データ | ||||||||||||||||||||||||||||||||||
| 緯度 | I9 | ??? ← 実際の緯度データ | ||||||||||||||||||||||||||||||||||
| x | J9 |
=IF(I9=0,RADIANS(H9-H$7)+$G$3*(H$6-1),COT(RADIANS(I9))* SIN((RADIANS(H9-H$7)*SIN(RADIANS(I9))))+$G$3*(H$6-1)) |
||||||||||||||||||||||||||||||||||
| y | K9 |
=IF(I9=0,0,RADIANS(I9)+COT(RADIANS(I9))* (1-COS(RADIANS(H9-H$7)*SIN(RADIANS(I9))))) |
||||||||||||||||||||||||||||||||||
| ↓ ↓ ↓ | ||||||||||||||||||||||||||||||||||||
| ↓ ↓ ↓ | ||||||||||||||||||||||||||||||||||||
| ============ 以下、ブロック数分を同様に繰り返す ============================================== | ||||||||||||||||||||||||||||||||||||
[図 6-3-8] 断裂多円錐図法
( 舟底型多円錐図法・Interrupted Normal Polyconic Projection )
【地図主点(中心)】東経 150゚、緯度 0゚ 【経度間隔】15゚【緯度間隔】10゚
セントラルワールドの民芸店(タイ国、バンコック 北緯13度44分49.38秒 東経100度32分23.43秒)
< Link to Google Earth & Map : 13°44'49.38"N,100°32'23.43"E >
あなたもジンドゥーで無料ホームページを。 無料新規登録は https://jp.jimdo.com から